
The first step is to work out how many layers the unit cell of the crystal has. Luckily, all you need are four lines in Python to start this up. Multiplying by equidistant atoms to cover the ones you don’t have requires knowledge of the lattice that we can’t easily work out for non-simple cubic arrangements. We’ll definitely need the full generator here though, and you can probably already see why: If we want to generate a complex lattice from a simple cubic, it’s better to have all the atoms to manipulate. Second, even once I did come across the more complete generator, despite its length, the original code still proved much faster in execution (and it had the added benefit of already been written). So why didn’t I use it back then? Two reasons: First, I liked the maths fun of figuring out the equidistant atom sequence, which turned out to be the number of ways to write an integer as the sum of three squares. If you’ve read my post on the Madelung Constant finder, you might notice that this snippet can actually do more than the entire generator I had in that post, since it actually covers all the coordinates in the lattice, circumventing the need for the “equidistant atom finder.” Triplets = list(itertools.product(S_range, repeat=3))Īx = fig.add_subplot(111, projection='3d')Īx.scatter(triplets, triplets, triplets, s = 200) Good question! But before we get into that, here’s a quick Python script that will generate simple cubic coordinates at increasing shell sizes S: But, how do you generate complex crystal lattice coordinates (if they aren’t already available online in a crystallographic database)? By nature, shouldn’t they be, well, complex ?
To simulate certain properties of a rigid lattice, a good method to employ is a direct numerical sum on a computer generated lattice, which usually converges as you add more atoms.

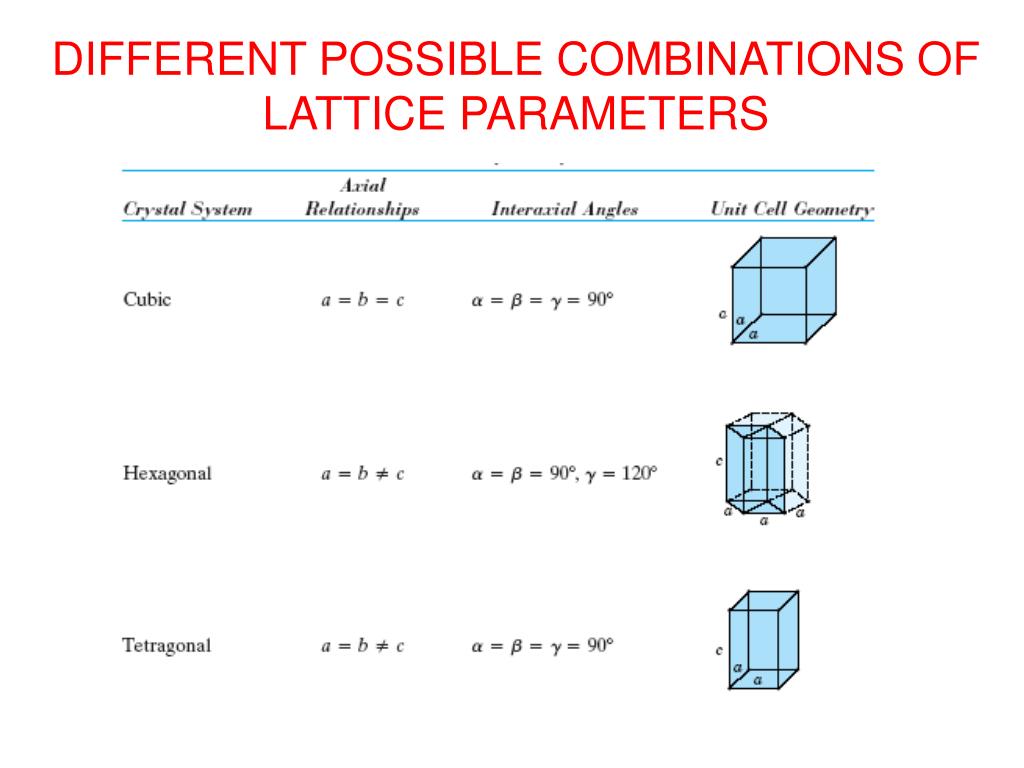
simple cubic, bcc, fcc and hexagonal structures). It’s generally pretty hard to find analytical solutions for properties of complex crystal lattices-by complex, I mean really anything outside the scope of your average CHEM 101 equivalent (i.e.


 0 kommentar(er)
0 kommentar(er)
